Photo: arthurized.photography

Research

My research focuses on the analysis of patterns that occur in nature. 

I use techniques and ideas from the theory of dynamical systems to study the emergence, existence, stability and dynamics of pattern-type solutions in systems of nonlinear partial differential equations, such as reaction-diffusion systems. 

Combining singular perturbations with geometric methods, I use analytical techniques to study the dynamics and interaction of patterns patterns in general classes of models, on curved and dynamical manifolds or spatially heterogeneous backgrounds. 

I'm inspired by pattern phenomena in biology, from subcellular to ecological scales. A major part of my work is developed in close collaboration with mathematical biologists, including interdisciplinary work with ecologists and cell biologists.

Research themes

Patterns on curved surfaces

How does the shape of a surface influence patterns on that surface? And what happens when a pattern determines the shape of the surface, creating a dynamical interaction? Mechanochemical pattern formation addresses these questions. Using geometrical and analytical methods, we can try to understand how patterns form on dynamically evolving backgrounds.
My main collaborators on this theme are Daphne Nesenberend (Leiden), Anna Marciniak-Czochra and Moritz Mercker (Heidelberg).

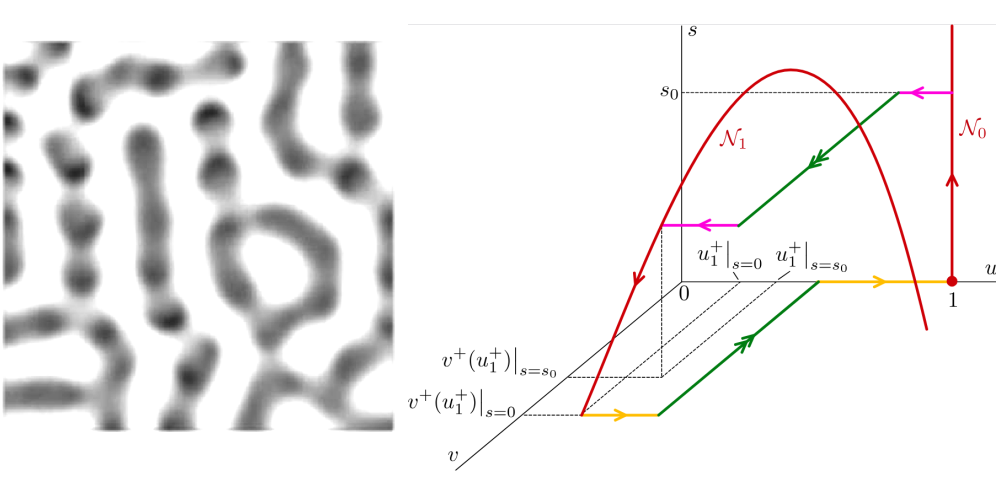
Multiple scale patterns

Scale separation in space and time is an important feature of many patterns, and of many models that have pattern-type solutions. Mathematically, we can use the theory of singular perturbations to study the hierarchy of scales in models, and describe the occurrence of spatial structures on multiple scales. We develop and apply these ideas in the context of cell biology, developmental biology and ecology.
My present and past collaborators on this theme include Annalisa Iuorio (Naples), Paul Carter (UCI), Nikola Popovic (Edinburgh) and Arjen Doelman (Leiden).

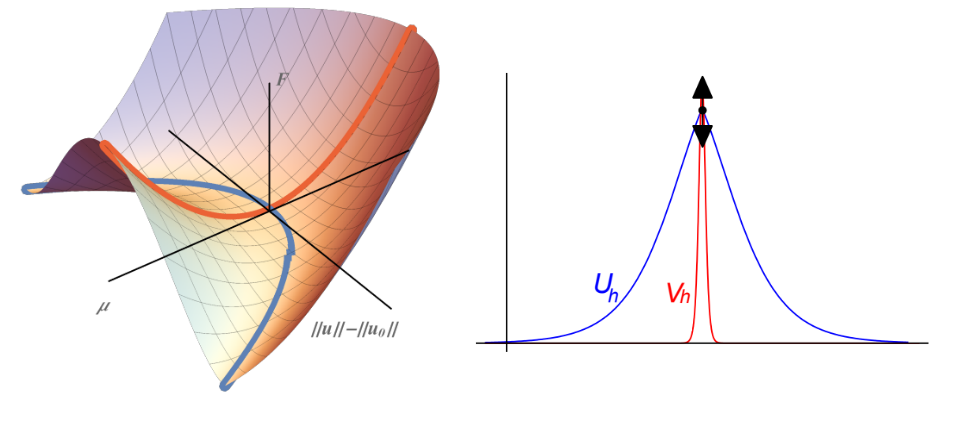
Controlling pattern stability

Stable patterns can be observed: analysis of pattern stability and dynamics proves an important link between predictions from mathematical models and physical or biological practice. What happens when a pattern becomes unstable, and how can we control its stability? Analytical methods based on scale separation are instrumental in addressing these questions, in particular in nonlinear, multi-component models for pattern formation.
My present and past collaborators on this theme include Isabelle Schneider (Berlin), Björn de Rijk (Karlsruhe) and Keith Promislow (MSU).

Publications

Recent talks